نیرو چیست؟؟؟

نیرو در فیزیک کمیتی برداری است که باعث شتاب گرفتن اجسام می‌شود. نیرو را به طور شهودی می‌توان با کشیدن یا هُل‌دادن توصیف کرد. شتاب جسم متناسب است با جمع برداری همهٔ نیروهای وارد بر جسم. در یک جسم صُلب (یعنی جسمی که ابعادش در فضا گسترده است و نمی‌توان آن را با یک نقطه تقریب زد) نیرو می‌تواند جسم را بچرخاند، تغییرشکل دهد یا فشار وارد بر آن را بیفزاید. اثرات چرخشی با گشتاور و تغییر شکل یا فشار با تنش توصیف می‌شوند. نیرو اثر متقابل دو جسم است.

نیروهای نابنیادی

خیلی وقت‌ها در توصیف پدیده‌ها از برخی جزئیات آن‌ها چشم می‌پوشیم. این کار باعث می‌شود بتوانیم مدل‌های ساده‌ای برای آن‌ها بسازیم و نیروهایی را تعریف کنیم که پدیده را به تقریب توصیف می‌کنند.

نیروی عمودبرسطح

وقتی جسمی را روی سطح همواری می‌گذاریم، نیروی گرانشی به آن وارد می‌شود. برای این که جسم در سطح فرونرود، نیرویی نیز از سوی سطح به جسم وارد می‌شود. این نیرو به خاطر رانش الکترومغناطیسی بین اتم‌های جسم و اتم‌های سطح است و نیروی عمودبرسطح نام دارد. مقدار این نیرو همیشه به اندازه‌ای است که نیروهای دیگر عمود بر سطح (مانند وزن جسم) را خنثی کند.

اصطکاک

نوشتار اصلی: اصطکاک

اصطکاک نیرویی است که با حرکت دو سطح نسبت به هم مخالفت می‌کند. مقدار این نیرو منتاسب است با نیروی عمودبرسطح بین دو جسم. در مدل‌های ساده‌شده، اصطکاک را در دو دستهٔ اصطکاک جنبشی و اصطکاک ایستایی رده‌بندی می‌کنند.

نیروی اصطکاک ایستایی $f_s$ وقتی دو جسم نسبت به هم ساکن‌اند به هر یک از دو جسم وارد می‌شود و دقیقاً مخالف نیرویی است که می‌خواهد دو جسم را نسبت به هم بلغزاند. این نیرو مقدار بیشینه‌ای دارد که با نیروی عمودبرسطح متناسب است:

$f_{s,max}=mu_s N$

ضریب تناسب 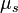$mu_s$ ضریب اصطکاک ایستایی نام دارد و وابسته به ویژگی‌های دو سطح است. مقدار نیروی اصطکاک می‌تواند بین صفر تا این مقدار بیشینه تغییر کند.

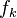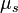نیروی اصطکاک جنبشی $f_k$ وقتی دو جسم نسبت به هم در حرکتند به هر یک از دو جسم وارد می‌شود و مقدار آن ثابت و برابر با $f_{k}=mu_k N$ است. این نیرو در خلاف جهت حرکت دو جسم نسبت به یکدیگر است و با حرکت آن‌ها مخالفت می‌کند. ضریب تناسب $mu_k$ ضریب اصطکاک جنبشی نام دارد و وابسته به ویژگی‌های دو سطح است. $mu_k$ معمولاً کوچک‌تر از $mu_s$ است.

مدل ساده‌شدهٔ بالا فقط به تقریب درست است. مثلاً در این مدل نیروی اصطکاک به مساحت تماس دو جسم وابسته نیست، حال آن‌که در عمل این نیرو به سطح تماس دو جسم بستگی زیادی دارد.

نیروی مقاوم شارّه

نیروی مقاومت شاره هنگامی که جسمی با سرعت در یک شاره (سیال) مانند آب یا هوا حرکت می‌کند به آن وارد می‌شود. این نیرو خلاف جهت حرکت جسم است و مقدارش تابعی از سرعت جسم است.

قوانین حرکت نیوتن

نوشتار اصلی: قوانین حرکت نیوتن

هر چند معروف‌ترین معادله ایزاک نیوتن 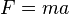$F = ma$ است، او در واقع شکل دیگری از قانون دوم حرکت خود، با استفاده از حساب دیفرانسیل ارائه کرد. در کتاب "Principia Mathematica"، نیوتن سه قانون حرکت ارائه کرده است که رابطه‌ای مستقیم با چگونگی توصیف نیروها در فیزیک دارند.

قانون اول نیوتن

قانون اول نیوتن درباره شرایط لازم برای سکون بحث می‌کند و به ویژه «اینرسی» را تعریف می‌کند که به جرم یک جسم مربوط است. با در نظر گرفتن ایده ارسطویی «حالت طبیعی»، شرط سرعت ثابت چه در حالت صفر و چه در حالت ناصفر، اینک «حالت طبیعی» اشیاء سنگین تلقی می‌شود. اشیاء به حرکت خود در حالت سرعت ثابت ادامه خواهند داد مگراینکه تحت تأثیر یک نیروی نامتعادل خارجی قرار گیرند.

قانون دوم نیوتن

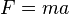اغلب نیرو را با استفاده از قانون دوم نیوتن، به صورت حاصلضرب جرم m در شتاب $vec a$ تعریف می‌کنند. فرمول $vec F = m vec a$ گاهی به عنوان دومین فرمول معروف فیزیک تلقی می‌شود. نیوتن هرگز $F = ma$ را به صورت صریح بیان نکرد، بلکه قانون دوم نیوتن در کتاب "Principia Mathematica" به صورت معادله دیفرانسیل برداری

$vec F = frac{d vec p}{dt} = frac{d(m vec v)}{dt}$

توصیف شده است، که در آن 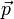$vec p$ اندازه حرکت سیستم است. نیرو میزان تغییر اندازه حرکت در واحد زمان است. شتاب میزان تغییر سرعت در واحد زمان است. این نتیجه که به صورت نتیجه‌ای مستقیم caveat در قانون اول نیوتن حاصل می‌شود، نشان می‌دهد که عقیده ارسطویی که یک نیروی شبکه‌ای لازم است تا یک شیئ در حال حرکت را با سرعت ثابت (و لذا با شتاب صفر) حفظ کند، به وضوح غلط بوده و فقط نتیجه یک تعریف نادقیق نبوده است.

استفاده از قانون دوم نیوتن به هر یک از صورتهایش به عنوان تعریف نیرو، در برخی از کتابهای درسی غیر دقیق تر، بی اعتبار معرفی شده است. زیرا این تعریف، همه محتویات تجربی را از قانون حذف می‌کند. در حقیقیت، 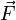$vec F$ در این معادله بیانگر یک نیروی شبکه‌ای (جمع برداری) است؛ در حال سکون، طبق تعریف، این بردار، صفر است. اما با این وجود نیروهایی متعادل موجود هستند و در واقع، قانون دوم نیوتن، نحوه تناسب شتاب و جرم را با نیرو بیان می‌کند که کدام یک از آنها را می‌توان بدون مراجعه به نیرو تعریف کرد. شتاب را می‌توان با با محاسبات حرکت‌شناسی (سینماتیک) تعریف کرد و نیز جرم را می‌توان مثلاً از طریق شمارش اتم‌ها تعیین کرد. اما با وجود اینکه سینماتیک در تجزیه و تحلیل‌های پیشرفته فیزیکی بسیار کارآمد است، هنوز سئوالات عمیقی وجود دارد از جمله اینکه تعریف دقیق جرم چیست؟ نسبت عام یک هم‌ارزی بین زمان فضای جرم معرفی می‌کند، اما بدون یک نظریه جامع گرانش کوانتومی، این هم‌ارزی گنگ می‌باشد چرا که معلوم نیست که آیا و چگونه این ارتباط در مقیاسهای میکروسکوپی برقرار است. با اندکی توجیه بیشتر، قانون دوم نیوتن را می‌توان به عنوان تعریف کمّی از جرم تلقی کرد به این صورت که قانون را به صورت یک تساوی نوشته، واحدهای نسبی نیرو و جرم را ثابت نگه داریم.

تعریف نیرو گاهی سئوال برانگیز است چرا که یا نهایتاً باید به درک شهودی ما از مشاهدات مستقیم رجوع کند یا به صورت ضمنی از طریق یک فرمول خودسازگار ریاضی تعریف شود. فیزیکدانان، فیلسوفان و ریاضیدانان معروفی که به دنبال تعریفی صریح تر از نیرو گشته‌اند، عبارتند از: Ernst Mach, Clifford Truesdell and Walter Noll.

پس از کسب موفقیت‌های تجربی، قانون نیوتن معمولاً برای اندازه‌گیری قدرت نیروها مورد استفاده قرار می‌گیرد. (برای مثال با استفاده از گردش‌های نجومی، نیروهای گرانشی اندازه‌گیری می‌شوند) با این وجود، نیرو و کمیتهایی که برای اندازه‌گیری آن مورد استفاده قرار می‌گیرند، همچنان مفاهیمی متمایز می‌باشند.

قانون سوم نیوتن

قانون سوم نیوتن، از به کار بردن تقارن در موقعیت‌هایی که نیروها را می‌توان به وجود اشیائی مختلف نسبت داده حاصل داده می‌شود. برای هر دو جسم (مثلاً ۱ و ۲) قانون سوم نیوتن بیان می‌کند که:

vec F_{12} = -vec F_{21}

این قانون بیان می‌کند که نیروها همواره به صورت عمل و عکس العمل رخ می‌دهند. هر نیرویی که از عمل شیئ ۲ به ۱ اثر می‌کند. به طور اتوماتیک با نیرویی همراه است که از عمل جسم ۱ بر روی جسم ۲ حاصل می‌شود. اگر اجسام ۱ و ۲ را در یک دستگاه یکسان در نظر بگیریم، نیروی شبکه‌ای روی سیستم حاصل از واکنش‌های بین اجسام ۱ و ۲، صفر است زیرا:

vec F_{12} + vec F_{21} = 0

این به این معناست که سیستم‌ها نمی‌توانند نیروهایی درونی تولید کنند که غیرمتوازن اند. اما اگر اشیاء ۱ و ۲ در سیستم‌های متمایز فرض شوند، آنگاه هر یک از این دو سیستم، نیروی نامتوازنی تجربه کرده طبق قانون دوم نیوتن نسبت به یکدیگر شتاب خواهد گرفت.

با ترکیب کردن قوانین دوم و سوم نیوتن می‌توان نشان داد که اندازه حرکت خطی هر سیستم محفوظ می‌ماند. با استفاده از $vec F_{12} = frac{d vec p_{12}}{dt} = -vec F_{21} = -frac{d vec p_{21}}{dt}$ و انتگرال گیری نسبت به زمان، معادله

mathcal {4} vec p_{12} = -mathcal {4} vec p_{21}

به دست خواهد آمد. برای سیستمی که شامل اشیاء ۱ و ۲ است، داریم

sum mathcal {4} vec p = mathcal {4} vec p_{12} + mathcal {4} vec p_{21} = 0

که همان محفوظ ماندن اندازه حرکت خطی را بیان می‌کند. تعمیم این حقیقت به یک سیستم مشتمل بر تعداد دلخواهی از ذرات، کاری سر راست است. این نشان می‌دهد که تغییر اندازه حرکت بین اشیاء موجود در یک سیستم، تأثیری روی اندازه حرکت سیستم نخواهد گذاشت. به طور کلی از آنجایی که همه نیروها ناشی از برهم کنش اشیاء صلب است، می‌توان سیستمی تعریف کرد که در آن اندازه حرکت شبکه‌ای نه هرگز از بین می‌رود و نه هرگز به دست می‌آید.